The possible angular momentum quantum numbers that result from combining two angular momentum quantum numbers
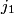 and and 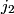 are are 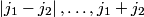 . The angular momentum quantum numbers that we need to combine in this problem are . The angular momentum quantum numbers that we need to combine in this problem are 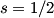 , , 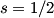 , , 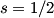 , , 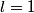 , and , and 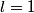 (three electrons with spin angular momentum quantum number (three electrons with spin angular momentum quantum number 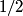 two of which are in a state with orbital angular momentum quantum number two of which are in a state with orbital angular momentum quantum number 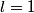 and one of which is in a state with orbital angular momentum quantum number and one of which is in a state with orbital angular momentum quantum number 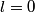 ). Therefore, the maximum total angular momentum quantum number is ). Therefore, the maximum total angular momentum quantum number is 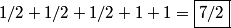 . . |